Generating ultra-short femtosecond pulses

Contacts:

Morten Bache, DTU Fotonik, 4525-3775 (moba@fotonik.dtu.dk)

Ole Bang, DTU Fotonik, 4525-6373 (oban@fotonik.dtu.dk)

http://www.fotonik.dtu.dk/staff/bache/

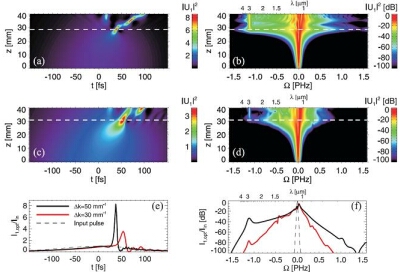Numerical simulation: (a) temporal and (b) spectral contents as a 200 fs pulse propagates with wavelength 1030 nm in a quadratic nonlinear crystal. The pulse eventually compresses to a 5.3 fs almost single-cycle pulse at the dashed line, see cut in (e) and (f) [black line]. (c) temporal and (d) spectral contents of a similar pulse, but propagating under stronger dispersion effects, which gives a much more poorer compression and pulse quality, see cut in (e) and (f) [red line].

Today common access to femtosecond pulses is ensured by mode-locked solid-state oscillators and the rapid advance in fiber lasers. However, the duration is typically around 100 fs and above, and for many applications shorter pulses are desirable. This is due to the fact that much higher intensities can be reached, and that applications in spectroscopy request ever shorter pulse durations. Therefore it is interesting to study efficient ways of compressing the pulses from standard fs oscillators. An extremely simple method is to use phase-mismatched second-harmonic generation. In this process the input pulse is frequency converted to the second harmonic (having twice the frequency of the input pulse), but due to the difference in the phase velocities of the two waves the conversion process is highly inefficient. Thus, very little light at the second harmonic frequency is generated. What is interesting is that the input pulse instead experiences a huge nonlinear phase shift, which generates a frequency chirp and eventually the dispersion in the nonlinear crystal compresses the input pulse using the soliton effect (see figure). This extremely short pulse is generated after propagating only a few cm in the nonlinear crystal, and opens up for common access to few-cycle fs pulses.

The project is theoretical and numerical. You will work on understanding the physics behind the compression process and will perform realistic numerical simulations of extreme nonlinear interaction of femtosecond optical beams.